Graph Traversal
1. Number of Islands (200)
Problem Description and Leetcode Link: The problem is called "Number of Islands" and the link to the problem on LeetCode is: https://leetcode.com/problems/number-of-islands/
Given a 2D grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example: Input: 11110 11010 11000 00000
Output: 1
Optimized Java Code with Detailed Comments:
class Solution {
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int numRows = grid.length;
int numCols = grid[0].length;
int numIslands = 0;
for (int i = 0; i < numRows; i++) {
for (int j = 0; j < numCols; j++) {
if (grid[i][j] == '1') {
numIslands++;
dfs(grid, i, j);
}
}
}
return numIslands;
}
private void dfs(char[][] grid, int row, int col) {
int numRows = grid.length;
int numCols = grid[0].length;
// Check if the current cell is out of bounds or not a part of the island
if (row < 0 || col < 0 || row >= numRows || col >= numCols || grid[row][col] == '0') {
return;
}
// Mark the current cell as visited (water)
grid[row][col] = '0';
// Explore adjacent cells (horizontal and vertical)
dfs(grid, row + 1, col); // Down
dfs(grid, row - 1, col); // Up
dfs(grid, row, col + 1); // Right
dfs(grid, row, col - 1); // Left
}
}Detailed Description of Algorithm and Thinking Process: The problem of counting the number of islands can be solved using a popular graph traversal algorithm called Depth-First Search (DFS). The idea is to traverse through the grid, and whenever we encounter a land cell (marked as '1'), we explore its adjacent cells using DFS to find the connected component (island) formed by that cell.
Here's how the algorithm works:
First, we check if the grid is empty or null. If it is, we return 0 as there are no islands.
We initialize variables for the number of rows, number of columns, and the number of islands.
We iterate over each cell of the grid and check if it is land ('1') or water ('0'). If it is land, we increment the island count by 1 and perform a DFS on the current cell.
The DFS function takes the current cell's row and column indices as inputs. It checks if the cell is out of bounds or if it is water ('0'). If either condition is true, it returns and stops the recursion.
If the cell is part of an island ('1'), we mark it as visited by changing its value to '0'.
We then recursively call the DFS function on the four adjacent cells: up, down, left, and right. This ensures that we explore the entire connected component (island) formed by the initial land cell.
Finally, we return the island count as the result.
During interviews, it is crucial to explain the algorithm step by step, describing the purpose of each code block and why it is necessary. Emphasize the use of DFS to explore the grid and find connected land cells. Also, mention the importance of marking visited cells as '0' to avoid counting them again. It's always a good idea to test the code with different examples to ensure its correctness and explain the time and space complexity. In this case, the time complexity of the algorithm is O(MN), where M and N are the number of rows and columns in the grid, respectively. The space complexity is O(MN) as well, due to the implicit call stack during recursion.
2. Course Schedule (207)
Problem description and problem link: Problem: Course Schedule (207) Link: https://leetcode.com/problems/course-schedule/
Description: You are given a list of courses, where each course is represented by a pair of integers [courseId, prerequisiteId]. There are a total of numCourses courses you have to take, labeled from 0 to numCourses-1.
Some courses may have prerequisites, for example, if prerequisites[i] = [a, b] this means you must take the course b before the course a.
Return true if it is possible to finish all courses, or false otherwise.
Optimized Java code with detailed comments:
Description on the algorithm and interview process:
The problem "Course Schedule" can be solved using graph traversal, specifically Depth First Search (DFS). The goal is to determine if there exists a cycle in the directed graph formed by the course prerequisites.
To solve the problem, we can follow the steps below:
Create an adjacency list to represent the graph: In the adjacency list, each course is represented by an index and the associated prerequisites are stored as adjacent nodes.
Populate the adjacency list with prerequisite relationships: Iterate over the prerequisites array and add the prerequisite courses to the adjacency list.
Track the status of each course: We need to keep track of the status of each course during the DFS traversal. We can use an array called "visited" for this purpose. Initially, all courses are marked as not visited (0).
Apply DFS traversal on each course: Iterate over the courses and for each unvisited course, perform a DFS traversal to check if there is a cycle. If a cycle is detected during the DFS traversal for any course, return false. Otherwise, return true.
During an interview, it's important to explain the overall approach to the problem and then dive into the details of each step. Interviewers often focus on evaluating the candidate's problem-solving skills and understanding of algorithms rather than just the code implementation. Therefore, it's vital to explain the algorithm using appropriate terminology and to demonstrate a clear thought process.
Additionally, it's beneficial to discuss the time and space complexity of the solution. The time complexity of this solution is O(V + E), where V is the number of courses and E is the number of prerequisites. The space complexity is O(V + E) as well, considering the adjacency list and the visited array.
Remember to test the code with different test cases and edge cases to ensure its correctness and efficiency.
3. Surrounded Regions (130)
Sure! Here is the optimized Java code for the LeetCode problem "Surrounded Regions" (130):
Problem Description: Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'. A region is captured by flipping all 'O's into 'X's in that surrounded region. The cells outside the surrounded regions should not be flipped.
Problem Link: https://leetcode.com/problems/surrounded-regions/
Java Code:
Explanation: The problem is solved by using a Depth-First Search (DFS) algorithm. The algorithm works as follows:
Check if the board is null or empty. If so, return.
Get the number of rows and columns in the board.
Traverse the first and last column and mark all 'O' cells and their connected 'O' cells as '*'.
Traverse the first and last row and mark all 'O' cells and their connected 'O' cells as '*'.
Traverse the entire board again, changing all remaining 'O' cells to 'X' and all '*' cells to 'O'.
During an interview, it's important to explain the algorithm step-by-step and highlight the key insights such as traversing the boundaries and marking the connected cells. Additionally, discussing the time and space complexity of the algorithm (which is O(rows * cols)) can also be beneficial.
4. Pacific Atlantic Water Flow (417)
Problem Description and Link: The problem "Pacific Atlantic Water Flow" is described as follows:
Given an m x n matrix of non-negative integers representing the height of each unit cell in a continent, the "Pacific Ocean" touches the left and top edges of the matrix, and the "Atlantic Ocean" touches the right and bottom edges.
Water can only flow in four directions: up, down, left, or right. Water flows from a cell to its neighboring cells with lower or equal heights.
Return a list of grid coordinates where water can flow from the Pacific to the Atlantic, or vice versa.
Problem Link: https://leetcode.com/problems/pacific-atlantic-water-flow/
Optimized Java Code with Comments:
Algorithm Explanation:
The problem can be solved with a depth-first search (DFS) approach.
To approach this problem during an interview, start by understanding the problem requirements and constraints.
Break down the problem into smaller sub-tasks. In this case, the sub-tasks are to determine the reachable cells from the Pacific Ocean and from the Atlantic Ocean.
Create a boolean matrix to track the reachable cells from each ocean.
Traverse the top and bottom rows, as well as the left and right columns, one by one, and mark each cell as reachable using the DFS algorithm.
Finally, check all the cells and add the ones that are reachable from both oceans to the result list.
During an interview, it is important to communicate your thoughts, explain the algorithm step by step, and discuss the time and space complexity of the solution.
5. Word Search II (212)
Problem Description:
The problem "Word Search II" (212) on LeetCode asks us to find all the words from a given list in a given two-dimensional board of letters. We can move in any of the four directions (up, down, left, or right) to form a word. The output should be a list of all the words that can be found in the board.
LeetCode Link to the problem: Word Search II
Optimized Java Solution with Detailed Comments:
Algorithm and Interview Thought Process:
The given problem can be solved using a backtracking algorithm along with a trie data structure. The backtracking algorithm is used to traverse each cell of the board, while the trie data structure helps in efficient word searching.
During an interview, here are the steps you can follow to approach and solve this type of problem:
Understand the problem statement completely and ask any clarifying questions if necessary.
Identify the key components of the problem and consider possible data structures to use. In this problem, the key components are the board and the list of words.
Think about how a trie data structure can be useful to speed up the process of word search on the board.
Implement the trie data structure and the backtracking algorithm.
During the implementation, pay attention to the control flow and ensure that all the required conditions are properly handled.
Test your implementation with different test cases, including edge cases, to validate its correctness and efficiency.
Optimize the solution if possible by identifying any redundant or unnecessary steps in the code.
Discuss the time complexity and space complexity of the solution, highlighting any trade-offs made.
Be prepared to explain your thought process and walk through the code during the interview. Provide clear and concise explanations, focusing on the algorithm's logic and how it solves the problem efficiently.
By following this approach and understanding the optimization techniques involved, you will be able to solve the "Word Search II" problem on LeetCode effectively.
Reorder Routes to Make All Paths Lead to the City Zero
There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.
This year, there will be a big event in the capital (city 0), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.
It's guaranteed that each city can reach city 0 after reorder.
Example 1:
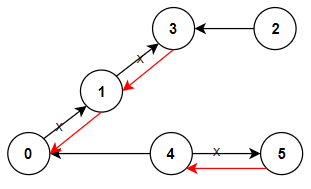
Solution:
Explaination:
Building the Graph:
We start by constructing an adjacency list representation of the tree. The graph is represented using a list of lists (
List<List<int[]>>). Each index in the list represents a city, and each element of the inner list represents an edge from that city to its neighboring cities. Each edge is represented by an array of size 2, containing the neighbor city and a flag indicating whether the edge is in the original direction (1) or reversed (0).
Depth-First Search (DFS):
We perform a depth-first search (DFS) starting from city 0, recursively visiting each city and its neighbors.
During the DFS traversal, we keep track of the number of edges that need to be reversed to reach city 0. We maintain a count variable initialized to 0.
At each step, when visiting a neighbor of the current city, we check whether the edge is in the original direction or reversed. If it's in the original direction (flag = 1), we increment the count by 1 because we need to reverse this edge to travel towards city 0.
We continue this process until we traverse all cities reachable from city 0.
Returning the Minimum Number of Edges Changed:
After the DFS traversal is complete, the count variable holds the total number of edges that need to be reversed to reach city 0 from all other cities.
We return this count as the minimum number of edges that need to be changed to enable every city to visit city 0.
Main Method:
In the main method, we create an instance of the Solution class and call the
minReordermethod with the provided parameters (number of citiesnand the array of connections).We then print the result obtained from the
minReordermethod.
Overall, the solution utilizes DFS to traverse the tree and counts the number of edges that need to be reversed to ensure that every city can visit city 0. It returns the minimum number of edges that need to be changed for this purpose.
Other solution
BFS solution:
Last updated